Los paquetes en R suelen estar orientados a obtener salidas gráficas escalables vectorialmente y de alta calidad. Sin embargo hay menos opciones para trazar formas sencillas basadas en píxeles sobre imágenes de mapa de bits (bitmap).
He construido una librería que permite "dibujar" las primitivas gráficas más básicas sobre un mapa de bits cargado como array, donde se codifica una luminosidad o color de píxel en cada elemento del mismo.
Entrecomillo "dibujar" porque el resultado no lo veremos hasta dar una salida raster (por pantalla o a fichero) a la matriz de imagen, cosa que por motivos de velocidad no hacen las funciones de la librería. En otras palabras, dibujamos a ciegas.

He construido una librería que permite "dibujar" las primitivas gráficas más básicas sobre un mapa de bits cargado como array, donde se codifica una luminosidad o color de píxel en cada elemento del mismo.
Entrecomillo "dibujar" porque el resultado no lo veremos hasta dar una salida raster (por pantalla o a fichero) a la matriz de imagen, cosa que por motivos de velocidad no hacen las funciones de la librería. En otras palabras, dibujamos a ciegas.

La matriz
En la salida (visualización y guardado) aplican los ejes cartesianos habituales. En la matriz las abscisas crecientes se corresponden con las filas y las ordenadas con las columnas, buscando una notación de acceso a los valores de los píxeles intuitiva en la forma

Los siguientes parámetros opcionales aportan versatilidad a la hora de dibujar o enviar la imagen a una salida:
img[] es la imagen en la que dibujamos. Las coordenadas sobre ella se dan en píxeles, admitiendo valores decimales que serán redondeados a la localización entera más próxima.En la salida (visualización y guardado) aplican los ejes cartesianos habituales. En la matriz las abscisas crecientes se corresponden con las filas y las ordenadas con las columnas, buscando una notación de acceso a los valores de los píxeles intuitiva en la forma
img[x,y].
Los siguientes parámetros opcionales aportan versatilidad a la hora de dibujar o enviar la imagen a una salida:
inc: modo de dibujado.inc=Tdibuja incrementando el valor de cada píxel,inc=Fdibuja sobreescribiendo el valor de cada píxel.val: valor con el que se dibuja en el píxel.fill: opción de relleno.fill=Trellena la forma geométrica,fill=Fdibuja solo el contorno.thick: grosor del trazo en píxeles. Solo tiene efecto sifill=F.trunc: normalización de valores.trunc=Trecorta a 1 los píxeles de valor superior a 1.gamma: curva gamma aplicada a la salida.
Para no caer en el uso de bucles empleamos la función
which(), acercándonos a la definición formal de lugar geométrico de los puntos que (which) cumplen ciertas condiciones.El uso de
inc=T aporta mucha flexibilidad porque al no sobreescribir el valor de cada píxel, sino incrementarlo en determinada cantidad, cualquier objeto gráfico plasmado en el array de imagen puede "borrarse" con tan solo dibujarlo de nuevo con el parámetro val en negativo. # Dibuja elipse img = DrawEllip(img, x0, y0, a, b, val=1) # Borra elipse img = DrawEllip(img, x0, y0, a, b, val=-1)
Esta opción incremental constituye una forma no destructiva de añadir y eliminar figuras en la imagen, donde los objetos supervivientes no se ven afectados por las eliminaciones. Además las primitivas se superponen sin ocultar la información preexistente, lo que funcionalmente es similar a un parámetro de transparencia.
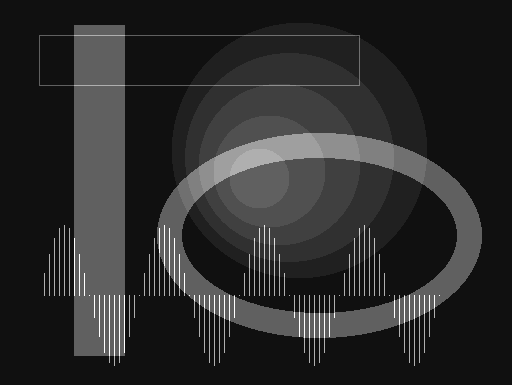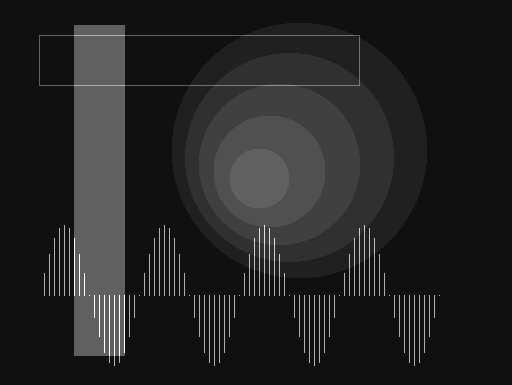
Todas las primitivas se dibujan sin antialiasing, lo que hace más visibles los dientes de sierra pero resulta más rápido y sencillo. Para el trazado de líneas se usa una rutina equivalente al algoritmo básico de Bresenham.
Como demostración he hecho una animación que sintetiza un diente de sierra aproximándolo con los cinco primeros términos de su desarrollo en serie de Fourier.
Como demostración he hecho una animación que sintetiza un diente de sierra aproximándolo con los cinco primeros términos de su desarrollo en serie de Fourier.
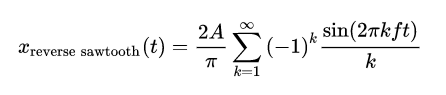
Fuente: Wikipedia
Las transparencias en los círculos que representan los fasores se logran con la modalidad de dibujo incremental (
inc=T). La funcion CopyRect() realiza el desplazamiento de la sección derecha sin necesidad de redibujar la gráfica para cada frame, solo se añade un dato nuevo en cada iteración (hacer clic para ver en alta resolución):
Se parametrizan dimensiones, número de períodos y términos de Fourier a calcular. El desarrollo con veinte términos de Fourier aquí, donde comienza a observarse el rizado de Gibbs en las discontinuidades del diente de sierra.
Y para terminar, un preliminar de otro proyecto donde las capacidades de transparencia de la librería facilitaron mucho la tarea de depurar cinemáticas de cierta complejidad.
La librería está planteada para tratar imágenes en escala de grises, aunque es sencillo adaptarla para trabajar en color (arrays de tres dimensiones en lugar de dos), pudiendo reutilizarse las funciones actuales.
Repositorio con el código R y archivos auxiliares: GitHub.
Y para terminar, un preliminar de otro proyecto donde las capacidades de transparencia de la librería facilitaron mucho la tarea de depurar cinemáticas de cierta complejidad.
La librería está planteada para tratar imágenes en escala de grises, aunque es sencillo adaptarla para trabajar en color (arrays de tres dimensiones en lugar de dos), pudiendo reutilizarse las funciones actuales.
~~~
Repositorio con el código R y archivos auxiliares: GitHub.



Excelente :)
ResponderEliminarHola ¿Cuál es el package que hay que instalar para poder utilizar estas funciones?
ResponderEliminarNinguno, no están dentro de ningún paquete. Basta ejecutar el código R del repositorio.
Eliminar