Simulación de solarigrafías con R

Para cerrar la trilogía de artículos dedicados al Sol que iniciamos en 'Localización del Sol por día y hora con R', vamos a calcular la proyección de la trayectoria solar sobre determinado soporte fotográfico. La solarigrafía (término inventado por Diego López Calvín, Sławomir Decyk y Paweł Kula), es un tipo de fotografía donde se busca capturar el recorrido del Sol a lo largo de un largo período de tiempo, días o incluso varios meses. Idealmente abarcará de solsticio a solsticio con el fin de capturar todo el rango de elevaciones.

Por su larga duración se realiza con película química empleando cámaras estenopeicas caseras, que en caso de colocarse en lugares públicos suelen esconderse y camuflarse para maximizar la probabilidad de supervivencia. Se obtienen imágenes de este tipo:

Fuente: Gianluca Belgrado (21-dic de 2018 a 16-jun de 2019)

Fuente: Regina Valkenborgh (21-jun a 21-dic de 2011)

Fuente: Csaba Kovács (11-ene a 25-feb de 2013)

Fuente: Greg Parker (18-jun a 21-dic de 2011)

~~~

Vamos a comparar las trazas solares que deberíamos obtener para tres configuraciones de cámara estenopeica:

• Cámara plana: clásica cámara estenopeica con proyección rectilínea (cámara oscura) ya que la película se dispone de forma plana. No es muy adecuada para solarigrafía por el limitado ángulo de visión que alcanza y estéticamente por el acusado estiramiento en los extremos.
• Cámara "lata": consiste en un cilindro con el estenopo sobre su superficie y la película adherida a la pared interior. Por facilidad de construcción (lata de refresco) es la más usada para realizar solarigrafías. Su proyección de tipo cilíndrico permite alcanzar ángulos de visión muy amplios, teóricamente cercanos a los 180º.
• Cámara "semilata": semicilindro con el estenopo centrado en la cara plana y película sobre pared curva interior. Alcanza el mismo ángulo de visión teórico de 180° de la cámara "lata". Pese a la mayor dificultad de construcción intuyo que tiene ventajas respecto a ella al garantizar un ángulo de incidencia más cercano a la ortogonal sobre la película, lo que debería facilitar alcanzar un gran ángulo de visión con calidad.

Formulamos las coordenadas de las proyecciones sobre la película correspondientes a cada posición angular del Sol para una orientación de las cámaras a sur (NOTA: todos los ángulos deben expresarse en radianes, si bien por claridad en las fórmulas aparecen en grados):

Que se resumen en fórmulas cerradas muy limpias:

Aunque como me apunta Valentín Sama, en una cámara estenopeica no aplica el concepto de distancia focal como tal, coincidimos en que si tuviéramos que elegir una dimensión que hiciera las veces sería f en la cámara plana, 2·R en la "lata" y R en la "semilata". A destacar solo viendo las fórmulas resultantes:

• La coordenada X de la proyección solo depende del Azimuth, siendo independiente de la Elevación en los tres modelos. En la "lata" y la "semilata" sigue además una proporcionalidad lineal con dicho Azimuth.
• La anterior propiedad tiene una consecuencia muy potente: cualquier sujeto rectilíneo paralelo al eje de la cámara se proyectará como una recta. Eso significa que si las cámaras "lata" o "semilata" se colocan perfectamente verticales (eje del cilindro perpendicular al suelo), cualquier edificio aparecerá recto, sin deformarse en el eje vertical.
• Adicionalmente en la "semilata" la coordenada Y solo depende de la Elevación, haciendo muy interesante su proyección porque cada eje refleja solo una coordenada angular (Azimuth → X, Elevación → Y). Se trata de la genuina proyección cilíndrica.
• La "lata" y la "semilata" tienen proyecciones bastante relacionadas: en el eje X son equivalentes (el factor 2 corrige la diferencia de focal), mientras en el eje Y la "lata" introduce un factor de compresión adicional (cos(Azimuth-180º)) respecto a la "semilata".
• Ese mismo factor cos(Azimuth-180º) aparece como divisor para la cámara plana, provocando una expansión en Y de las trazas.
• Para la dirección sur (Azimuth=180º), las tres cámaras realizan proyecciones equivalentes: la coordenada X vale 0 y la coordenada Y equivale a la distancia focal multiplicada por la tangente de la Elevación.

~~~

Conocidas las fórmulas veamos cómo proyectaría una solarigrafía cada modelo de cámara. Para hacer las dimensiones de los resultados comparables igualaremos distancias focales:

f = 2·Rlata = Rsemilata

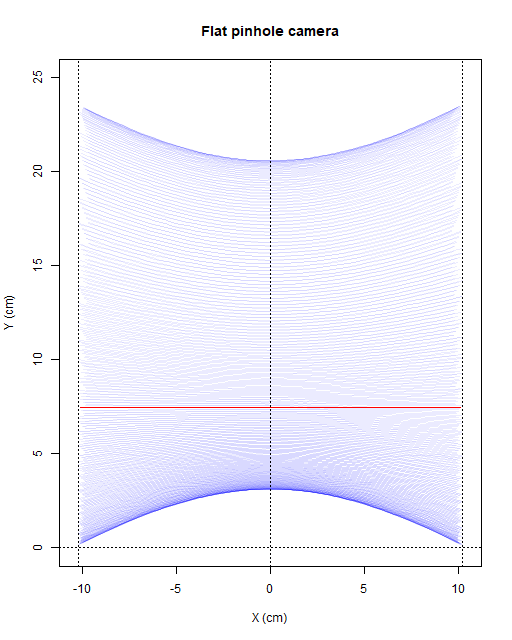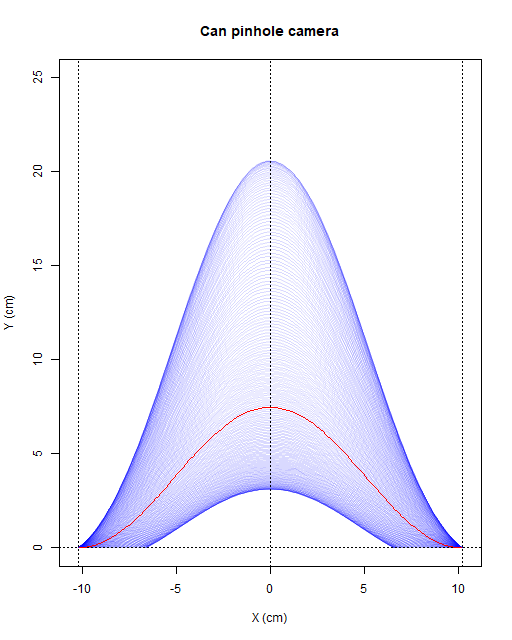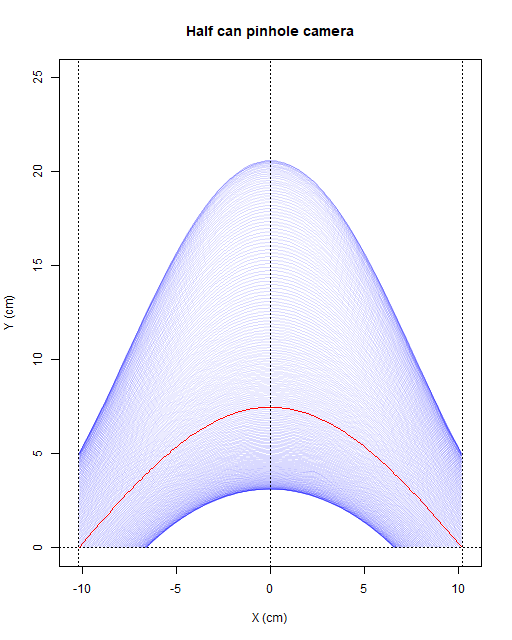
Tomando como referencia las dimensiones de una lata de refresco estándar, que tiene un diámetro de 6,5cm, modelamos para: f=6,5cm, Rlata=3,25cm y Rsemilata=6,5cm. Las curvas obtenidas con las dimensiones de película química requerida en cm resultan (clic para alta resolución):

La cámara rectilínea es la única que plasma las trayectorias en línea recta del Sol en los equinoccios (marcados en rojo en las gráficas). Por otra parte como se puede deducir de la morfología de las tres cámaras probadas, todas realizan exactamente la misma proyección para rayos con Azimuth=180º (que corresponde a X=0cm en la gráfica).

Se puede considerar que la cámara "semilata" tiene un comportamiento intermedio entre la "lata" y la cámara plana. La diferencia más notoria es que al acercarnos a los extremos del ángulo de visión, la compresión en Y de la cámara "lata" lleva a 0 todas las curvas cuyo Azimuth sobrepase los 90º/270º, perdiendo toda la información de Elevación, cosa que no hace la "semilata".

Las trazas de la "lata" y la "semilata" son equivalentes en ángulo de visión abarcado en horizontal con un FOV=180º. La cámara lineal en cambio tiene un ángulo de visión en horizontal menor que depende de la focal y ancho de película usada. En nuestro caso como asumimos la misma focal y dimensiones de película en las tres cámaras:

MAXX = 6,5·π/2 = 10,2cm

FOVplana = 2·atan(MAXX/6,5) = 2·atan(π/2) = 115º

Es decir para una misma focal y ancho de película la cámara lineal abarca un FOV=115º (área coloreada), el 64% del que logran sus rivales:

~~~

Podemos comprobar la corrección del cálculo de la cámara "lata" comparando sus curvas con la imagen del inicio de Gianluca Belgrado (él usó un tubo de PVC), ya que su foto está hecha en Casarano (Italia), prácticamente en la misma latitud que nuestro estudio (sierra de Madrid), lo que hace que ambas localizaciones compartan trayectorias solares.

Gianluca parece que tenía claro su objetivo: fue cuidadoso de apuntar la cámara exactamente a sur, colocó el estenopo a la altura de la parte superior de la película para desplazar el ángulo de visión por encima del horizonte, y usó película del tamaño suficiente para capturar las curvas más altas del solsticio de verano (hacer clic para mayor resolución):

La correspondencia entre los cálculos y la foto es sorprendentemente precisa. Comparando con el límite de 180º estimamos un ángulo de visión en horizontal nada despreciable de FOV=153º, demostrando que la cámara "lata" puede plasmar rayos muy tangenciales:

~~~

En otra solarigrafía el mismo Belgrado utilizó una "semilata" obteniendo un resultado acorde a las proyecciones calculadas:

Fuente: Gianluca Belgrado (agosto a diciembre de 2021)

La cámara se escondió tras un robusto poste de señalización, lo cual ayudó a obtener una perspectiva perfectamente vertical de los edificios. Puede verse el estenopo descentrado hacia la mitad superior para capturar más porción por encima del horizonte que por debajo:

Fuente: Gianluca Belgrado

La orientación ligeramente descentrada a sureste hizo que las trazas de la salida del Sol aparezcan casi completas a perjuicio de las puestas. Esto me da una idea para capturar el recorrido solar completo hasta en el solsticio de verano, realizar una panorámica con dos "semilatas" rotadas entre sí al menos 90º:

Una capturará los amaneceres y otra las puestas de Sol. Para montar la panorámica bastará superponer las dos películas, realizable incluso en el dominio químico. Que la coordenada Y en la "semilata" solo dependa de la Elevación hará que cortemos donde cortemos, incluso sin seguir una trayectoria lineal, la imagen final será la misma. En los sujetos más cercanos se producirá algo de inevitable error de paralaje, pero las trayectorias solares por su lejanía deberían casar a la perfección.

~~~

Vamos a ver cómo proyectaría cada cámara los analemas solares. Un analema es la curva de tipo lemniscata (forma de ocho) generada por la secuencia de las posiciones del Sol a lo largo del año a una misma hora del día (obviamente sin correcciones de horario de verano/invierno), contemplado desde una posición fija.

De los 24 analemas correspondientes a las horas del día aproximadamente solo la mitad resulta visible por caer los demás por debajo de la línea de horizonte, así como por las limitaciones de ángulo de visión de las cámaras usadas (clic para alta resolución):

La cámara "semilata" respeta mucho mejor la forma de los analemas que la cámara "lata" al alejarnos del centro (dirección en la que apunta la cámara, en este caso sur). Esto da una idea de la gran distorsión general que provoca la cámara "lata" sobre las trayectorias solares. También notamos en esta gráfica el menor ángulo de visión de la cámara plana, reflejado en el hecho de que para un mismo tamaño de película abarca un menor número de analemas que las otras dos.

Aquí la imagen del primer analema fotografiado sobre una misma película, 44 exposiciones hechas a la misma hora durante 1978-79. El autor usó una cámara de proyección rectilínea apuntada a la porción de cielo donde se dibujaría el analema, de ahí su baja distorsión. Incluyó trazas parciales de los solsticios y del punto central, toda una virguería:

Fuente: Dennis di Cicco

Y terminamos con un analema múltiple añadiendo una traza completa en lo que pudiera ser el equinoccio:

Fuente: Steve Riegel

De la baja distorsión de los analemas en los extremos deducimos que no podía tratarse de una cámara "lata" clásica, pero es que el propio autor explica que usó una "semilata":

Fuente: Steve Riegel

~~~

En conclusión la "semilata" parece un mejor diseño para producir solarigrafías que la más usada "lata" de refresco (o similar forma cilíndrica) al tener las siguientes ventajas:

• Distorsión mucho menor en los extremos evitando perder información de Elevación y respetando la forma de los analemas.
• Ángulos de visión más cercanos al máximo teórico de 180º al trabajar con ángulos de incidencia sobre la película menos severos.
• Realiza una proyección cilíndrica estándar, representando el Azimuth independiente de la Elevación al plasmar cada uno sobre un eje de coordenadas diferente.
• Facilidad para realizar panorámicas de montaje inmediato capturando el recorrido completo del Sol en el solsticio de verano.

El coste obviamente está en una mayor complejidad de fabricación de la cámara.

~~~

Con la cámara "semilata" los ángulos de incidencia sobre la película se hacen menos rasantes, pero en el estenopo las cosas resultan igual de críticas que con cualquier otra cámara.

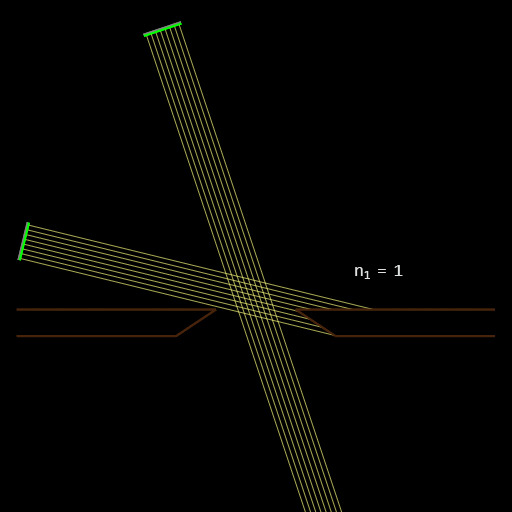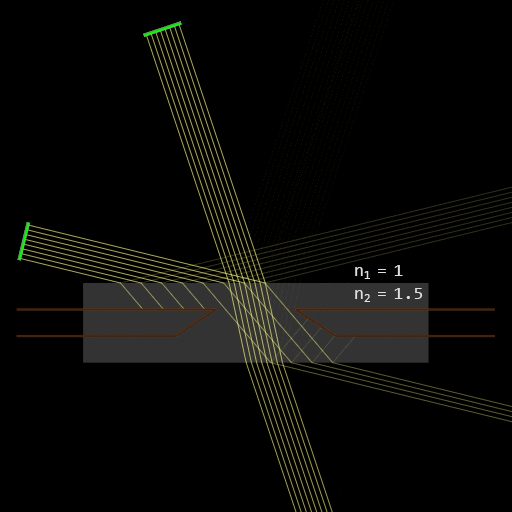
Una mejora que se me ocurre es aprovechar la refracción en un material pulido de mayor índice de refracción que el aire (plástico, adhesivo óptico,...) que, envolviendo el estenopo, logre hacer más llevaderos los ángulos con los que la luz atraviesa el orificio y sin alterar el ángulo final de incidencia sobre la película.

En esta simulación hecha con Ray Optics Simulation vemos cómo el material altamente refractivo logra salvar rayos que con el estenopo "en seco" no lograban penetrar en la cavidad:

Una posible implementación con dos cubreobjetos sugerida por Valentín Sama garantizaría superficies lisas y pulidas. Podría usarse Superglue (de igual índice de refracción que el vidrio según el fabricante) para hacer la doble función de rellenar el estenopo y pegar los cubreobjetos al material:

Esto es todo teoría óptica de trazado de rayos. En el mundo real la incógnita será lo que pueda llegar a pasar con todas esas reflexiones o la calidad del cianocrilato como material óptico...

~~~

Repositorio con el código R: GitHub.